Blog 4: Design of Experiments (DOE)

CASE STUDY

What could be simpler than making microwave popcorn? Unfortunately, as everyone who has ever made popcorn knows, it’s nearly impossible to get every kernel of corn to pop. Often a considerable number of inedible “bullets” (un-popped kernels) remain at the bottom of the bag. What causes this

loss of popcorn yield? In this case study, three factors were identified:

1. Diameter of bowls to contain the corn, 10 cm and 15 cm

2. Microwaving time, 4 minutes and 6 minutes

3. Power setting of microwave, 75% and 100%

Factor Designation	Factor	+	-
A	Diameter	15cm	10cm
B	Microwaving time	6 min	4 min
C	Power	100%	75%

8 runs were performed with 100 grams of corn used in every experiments and the measured variable is the amount of “bullets” formed in grams and data collected are shown below:

Factor A= diameter

Factor B= microwaving time

Factor C= power

Run Order	A	B	C	Bullets (grams)
1	+	-	-	3.48
2	-	+	-	2.48
3	-	-	+	0.74
4	+	+	-	1.48
5	+	-	+	0.95
6	+	+	+	0.32
7	-	+	+	0.48
8	-	-	-	3.12

FULL FACTORIAL

Significance of Factors

The highs and lows for each factor from the tabulated data are summed and averaged out. The average highs and lows are used to plot the graph below. The graph helps to visualize the differences in the highs and lows of each factor and hence their significance through the difference in gradients shown.

When Diameter increases from 10cm (-) to 15 cm (+), the average mass of the bullets decreases from 1.705g to 1.5575g.

When Microwaving Time increases from 4 min (-) to 6 min (+), the average mass of the bullets decreases from 2.0725g to 1.9g.

When Power increases from 75% (-) to 100% (+), the average mass of the bullets decreases from 2.64g to 0.6225g.

C (Power) has the largest effect / significance, followed by B (Microwaving Time), then A (Diameter). A higher significance means that the factor affects the variable more, i.e. a larger change in the value of the measured variable per unit change in the factor. The gradients and differences reflect as such and factor C has the largest gradient and difference between its high and low values.

Interaction Effects

Two factors are selected and their data is analyzed to help picture how they interact with one other. When two factors chosen, at scenarios where the first factor has a low and high value, the data of the second factor will be be tabulated for those scenarios to plot a graph accordingly. By comparing the gradients of the graph, we will know the significance of the interaction.

A x B

The gradient of both lines are different in that one is a positive gradient and the other is a negative gradient. Therefore, there is a significant interaction between A (Diameter) and B (Microwaving Time).

A x C

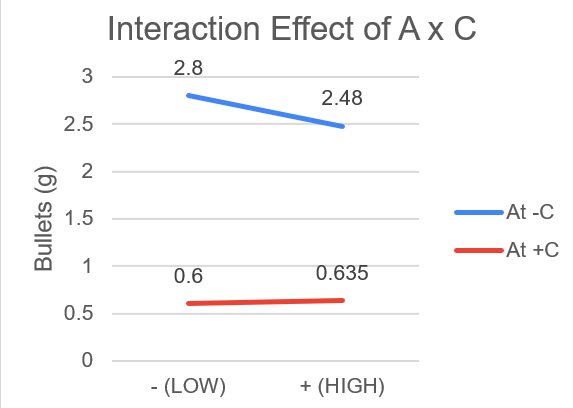
Although the gradient of both lines are different in that one is a positive gradient and the other is a negative gradient, the gradients of less different when compared to A x B. Therefore, there is a significant interaction between A (Diameter) and C (Power Setting) but not as much as interaction as A (Diameter) and B (Microwaving Time)

B x C

The gradients of both lines are very similar. Therefore, the interaction between B (Microwaving Time)and C (Power Setting) is small.

Conclusion

The most important factor is power, then microwaving time, then diameter.

More corn will pop when the bowl's volume increases due to an increase in diameter. The more corn in the microwave, the more popcorn and bullets there will be. The quantity of bullets, however, really fell. This is unexpected, but it's also possible that it's because not every bag of microwaveable popcorn is the same, and because the microwave is ultimately responsible for popping the popcorn, diameter isn't that important.

Fractional Factorial

Instead of the full 8 runs, 4 runs are chosen instead to maximize the efficiency of the analysis. The runs chosen were 1, 2, 3 and 6. These runs were chosen as in these runs, all factors, both high and low occur the same number of times.

When Diameter increases from 10cm (-) to 15 cm (+), the average mass of the bullets increases from 1.6g to 1.9g.

When Microwaving Time increases from 4 min (-) to 6 min (+), the average mass of the bullets decreases from 2.11g to 1.4g.

When Power increases from 75% (-) to 100% (+), the average mass of the bullets decreases from 2.98g to 0.53g.

C (Power Setting) has the largest effect / significance, followed by B (Microwaving Time), then A (Diameter).

Conclusion

In terms of the significance of each factor, the results of the fractional factorial are the same as the full factorial which is why fractional factorial is efficient and time-saving.

However, the results also show its disadvantage in risking missing information. When using the fractional factorial method, the number of bullets increased when A increased, which is different from the full factorial method which showed a decrease instead.

The excel file I used for the calculations is attached below

CPDD DOE BLOG.xlsx

Download XLSX • 38KB

DOE PRACTICAL

The DOE practical was one of those practical sessions I would consider more on the fun side as is with many ICPD or CPDD practical sessions. I would say it was even funner than that one ICPD practical where we learnt about cardboard construction techniques and constructed a random cardboard contraption. In the practical, we were tasked to perform DOE with a toy catapult. My group of 5 members were split into two smaller groups of 3 and 2, with myself being in the former. The former group was to do a full factorial analysis while the smaller group a fractional factorial. At the end of the session, a surprise group challenge awaited us...

For the catapult, the three factors used for DOE were

The values from the arm length were derived from measuring the lengths of the two different armatures provided and same with the projectile weight. The stop angle values were derived by measuring the angle of the arm relative to the ground. The angle was measured from where the arm pivoted.

The projectiles provided. The brown was the lighter one (-) and the red was the heavier one (+).

We conducted the experiment by placing the catapult and tray of sand on the ground. The catapult would launch the projectile into the sand and then we would measure the distance the projectile traveled by measuring the center of the crater created and the pivot of the catapult arm. This was the more boring part of the practical as we had to constantly stand up and sit down and my legs were not having a good time.

After what felt like 1000000 years, we finally had all the data we needed for a full factorial analysis.

When A (Arm Length) increases from 28 to 33 cm, the average distance travelled by the projectile decreases from 80.36 to 62.15 cm.

When B (Projectile Weight) increases from 0.8619 to 2.0117 g, the average distance travelled by the projectile decreases from 75.66 to 66.85 cm.

When C (Stop Angle) increases from 10° to 40°, the average distance travelled by the projectile decreases from 94.33 to 48.18 cm.

Stop angle is the most significant factor, followed by arm length, then projectile weight.

Group Challenge

This is where the fun part was. For the group challenge, we were tasked to use the data we gathered to shoot a bunch of mini targets down on a lab table. At first, I was rather worried as the largest distance traveled in our data did not exceed 1m and the targets we were presented were very far away. Furthermore, it was also a competition between the other groups in the class meaning there were marks at stake. For the rules of the game, we were give 3 total trial shots that we could use at any time. However, we had to announce whether it was a trial shot or an actual attempt before we fired. We had two attempts per target. If the shot landed on a trial shot, it would not count and we would have to take another shot and declare it as an attempt.

The above diagram is what the lab table looked like. (Courtesy of Dylan)

For some reason my group made me man the catapult. :(((

For the first target, we decided to actually use our data to calculate the most optimal shot. Our first shot was a trial shot which unfortunately missed. Our second shot was another trial shot which thankfully hit the target and we used our attempt for the next shot. 1 down and 3 to go.

For the second target, we also used math to gauge our shot and our first shot was our very last trial shot. Unfortunately we had missed and used all our trials for the game. Even more unfortunate was that our 2 actual attempts also missed.

The third target was considered difficult because it was behind a covered electrical socket and thus, the catapult had to be angled to shoot it. For our shots, we had to tilt our catapult such that it had to shoot the target diagonally. For our first shot, we missed as the ball bounced too high. I decided to increase the stop angle to reduce the power of the shot and managed to hit the target on the last attempt.

For the last target, our data couldn't help us as the target was too far away. So we had to hail Mary our last two shots. For our first shot, we missed it as it landed right in front of the target and bounced over. My team was frantically trying to use our data to somehow extrapolate the factors we needed to use as we had only hit two shots so far which would tie us with another group our friends were in. Obviously we couldn't let that happen as they were praying on our downfall when they were watching us and we needed to take the W and rub it in their faces. As the ball hit the table right in front of the target, I just winged it by cranking the arm one peg down and launching it and had hit the target, much to the shock of myself and my lecturers. They should make me a marksman when I enlist.

Our group managed to take FIRST place as we had downed 3 targets while all the other groups downed 2.

Reflections

The DOE practical was rather repetitive but the group challenge was definitely fun and probably a memory I'll never forget. Hitting the last target followed by a 'how did you do that?!' from Mr Chua was very gratifying. And to answer your question Mr Chua, I am simply that good. On a more serious note, I understand how DOE applies to the real world as DOE can be used to design equipment in the engineering sector. For example, trying to improve the efficiency of a heat exchanger. We first look at the factors that affect the efficiency, run a few tests and use DOE to decide which factor to focus on. On a small scale test like the group challenge, I was able to randomly guess the stop angle for the catapult to make a seemingly impossible shot, but for something that is a one time hit-or-miss like sending a spacecraft into outer space, guessing is out of the question.